O obxetivo do exercicio é ordear unha colección de fideos por orde crecente de lonxitude, é dicir, desde o máis curto ó máis longo. A primeira parte do exercicio permite manipular coas mans, xa que a manipulación de materiais permite entender mellor os procesos e conceptos. Esta parte é adecuada para o alumnado de todos os niveis, para entender como funcionan as máquinas e como temos que diseñalas. Para o alumnado máis novo hai unha actividade que atoparás ó final deste obradoiro (ou pulsando aquí) e que pode axudar a facer máis lúdico o exercicio.
Iremos incrementando a dificultade para relacionalo coa construción de programas, e esta parte xa é máis recomendable para o alumnado de niveis superiores (ESO ou incluso bacharelato). Corresponde ó profesorado decidir ate onde chegar en función dos seus obxectivos.
Comezamos repartindo tres fideos a cada persoa (se é alumnado moi novo, podes facelo con dous, e se é alumnado maior con catro), como se amosa a continuación (figura 1):

Figura 1. Materiais para a realización do exercicio ordeando fideos. Foto de Noelia Gallego
Rompemos cada fideo en dous trozos, de xeito que teñamos 6 metades de distinta lonxitude. Poñemos todas as metades desordeadas por lonxitude sobre a mesa, de xeito que se perciba con claridade que son 6 fideos de distinta lonxitude (figura 2):

Figura 2. Disposición das seis metades de fideos sobre a mesa. Inicio da resolución do problema. Foto de Noelia Gallego
Teñamos presente que o problema que se nos formula é ordear os fideos por orde crecente de lonxitude (na esquerda o fideo máis curto e na dereita o fideo máis longo). Se lle formulamos este problema ó alumnado, todos saben resolvelo.
Pero queremos indagar en como o fixeron para despois replicar o proceso e, así, ensinarlle ó ordenador a resolver esta tarefa (mediante un programa).
Preguntemos entón…. «que mecanismo usaches para acadar a solución?» Probablemente non obteñas resposta, porque resolvemos o problema sen ser conscientes de como o facemos («resulta algo obvio, como podes preguntar isto!»). O ordeamento por lonxitude debe ser algo que facemos a miúdo desde que nacemos e resolvemos a tarefa sen pensar como. É como se usaramos unha memoria visual/gráfica inconsciente.
É evidente que unhas instrucións vagas e ambigüas non permiten ensinarlle ó ordenador a resolver o problema. Imos ver a continuación como o fan os ordenadores (hai inventados varios algoritmos que fan esta tarefa, imos usar o algoritmo de selección, pero o nome non lle importa nada ó noso alumnado). O algoritmo (tamén podemos chamalo mecanismo ou estratexia) danos instrucións de que temos que facer para chegar á solución do problema:




Figura 3. Señálamos o primeiro fideo comezando pola esquerda (superior), fideo a intercambiar (segunda), intercambio dos dous fideos señalados (terceira) e resultado despois do intercambio (inferior). Fotos de Noelia Gallego
O algoritmo comeza sinalando o primeiro fideo da esquerda da colección (ver figura 3 superior). Seguinte paso é percorrer (mirar) os fideos que están a dereita do sinalado (desde o sinalado ate o final da colección) e sinalar aquel con menor lonxitude (ver segunda foto da figura 3). Finalmente, intercambiar ambos fideos señalados (terceira imaxe da figura 3). Con este proceso, o primeiro fideo da esquerda xa está ordeado, porque é o máis curto da colección (última imaxe da figura 3).




Figura 4. Repetición do proceso da figura 3 para o segundo fideo comezando pola esquerda. Fotos de Noelia Gallego
O seguinte paso será repetir o proceso da figura 3, pero comezando polo seguinte fideo (o segundo fideo comezando pola esquerda, xa que o primeiro xa o temos ordeado). A figura 4 visualiza este proceso. Primeiro, señalamos o seguinte fideo non ordeado (segundo fideo comezando pola esquerda) como na imaxe superior da figura 4, avanzamos toda a colección de fideos cara á dereita ata atopar o fideo máis curto deste percorrido (segunda foto na figura 4). Xa é tempo de intercambiar ambos fideos seleccionados (terceira foto da figura 4). Finalmente, vemos o resultado na foto inferior da figura 4, na que os dous primeiros fideos comezando pola esquerda están ordeados.



 Figura 5. Repetición do proceso das figura 3 e 4 para o terceiro fideo comezando pola esquerda. Foto de Noelia Gallego
Figura 5. Repetición do proceso das figura 3 e 4 para o terceiro fideo comezando pola esquerda. Foto de Noelia Gallego
Seguimos repetindo o mesmo mecanismo para o terceiro espagueti comezando pola esquerda, tal como se pode observar na secuencia de imaxes da figura 5. Neste punto xa nos damos conta de que, en cada repetición do proceso, un novo fideo queda ordeado. Nesta figura 5 xa están ordeados de menor lonxitude a maior os tres primeiros fideos da colección.



Figura 6. Repetición do proceso para o cuarto fideo comezando pola esquerda. Foto de Noelia Gallego
Observamos que para que toda a colección quede ordeada, temos que repetir o proceso tantas veces como elementos ten a colección, no noso caso 6. A figura 6 amosa outra repetición deste proceso para ordear o cuarto fideo comezando pola esquerda. Teriamos que repetir o proceso co quinto fideo, pero comprobamos que xa está ordeado e que non temos que intercambiar máis fideos (ver figura 7). Isto de “repetir un proceso ou mecanismo un número coñecido de veces (6)” xa nos soa do obradoiro 9.

Figura 7. Amosa a solución do problema, os fideos están ordeados desde os máis curtos ós máis longos (orde crecente de lonxitude do fideo). Foto de Noelia Gallego
A primeira vez que realices o proceso que acabo de describir, podes usar a mesma situación inicial da parte superior da figura 3 usada neste exemplo, coa finalidade de que o alumnado non se perda e que as instrucións sexan claras. Despois, podes repetir algunhas veces o experimento para que o alumnado se familiarice coa filosofía de resolución das máquinas (sempre fan as mesmas instrucións, nunca saltan ningún paso, como algunhas veces facemos as persoas cando dominamos unha tarefa). Podes presentalo como un pequeno xogo por parellas, onde unha persoa desordea os fideos e a outra os ordea, e despois mudan os papeis. Tamén é importante indicarlles que se fixen no detalladas que son as instrucións para resolver o problema ou tarefa, lembrándonos esa idea de que ensinarlle a un ordenador a resolver problemas simples é como ensinar a bebés ou alumnado de infantil.
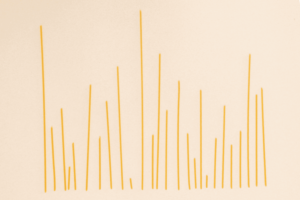
Figura 8. Nova colección de fideos para ordear. Foto de Noelia Gallego
Se agora puxeramos moitos máis fideos, como se amosa na figura 8, saberiamos ordear esta nova colección de fideos? Podes preguntar ó alumnado, pero, previsiblemente, a resposta será “si”. Podemos facelo, pero xa non é unha tarefa que nos pareza divertida porque é pesada, xa que agora hai que repetir moitas veces o proceso, teño que concentrarme moito e cánsame. Sabería facela un ordenador? Levaríalle moito tempo? Considerando que para o ordenador o problema é ordear unha colección de números, onde cada número é a lonxitude do fideo, a súa resolución sería instantánea para coleccións con 1000 ou incluso un millón de números. Polo tanto, vemos que as máquinas poden axudar a facer tarefas moi rápido e sen cansarse.
Xa nos familiarizamos co problema e a solución que utilizan as máquinas, pero…. o ordenador usa a intelixencia artificial ou aprendizaxe automática na resolución deste problema? A resposta é NON.
A única intelixencia que hai na resolución deste exercicio é a da persoa (non coñezo o seu nome) que inventou este algoritmo de ordeamento, que aporta unhas instrucións unívocas (que non son ambigüas) que sempre levan á solución do problema.
Pero… como resolveriamos na linguaxe de programación Python este problema? A continuación descríbense varios programas en Python que van aumentando o nivel de dificultade. Tal vez estes exercicios xa só sexan interesantes para o alumnado de ESO ou bacharelato (o profesorado será quen decida).
Para facer estes exercicios, descarga esta carpeta .zip na que atoparás varios arquivos ós que me referirei ó longo deste obradoiro.
Afortunadamente, Python xa ten unha función que realiza o problema (é a función sort( )) como vedes na figura 9. Podes escribir o programa no interprete de Python en internet (aquí) ou pulsar no primeiro botón da barra de ferramentas e abrir o arquivo Obra10Prog1.py que che proporciono. Se pulsas o botón Run, ves no panel inferior o resultado da execución do programa.
A continuación, a explicación do código para o profesorado:
- A liña 1 é un comentario.
- A liña 2 introduce as personaxes do noso teatro (un teatro non pode desenvolverse sen personaxes e cada un ten un nome). Na narrativa da programación, os personaxes chámanse variables, pero isto non lle importa moito á infancia; xa teremos tempo a aprender nomes raros. O personaxe con nome “numeros” dámoslle (asignámoslle) unha colección de números (que aparece entre corchetes e separada por , porque así son as regras da linguaxe de programación Python). Estes números serían as lonxitudes dos fideos.
- A liña 3 mostra a lista de números utilizando a función print().
- A liña 4 fai o ordeamento da colección de números en orde crecente (de menor a maior valor) utilizando a función sort().
- A liña 5 visualiza ou mostra o resultado, que será o valor que ten agora a personaxe “numeros”.
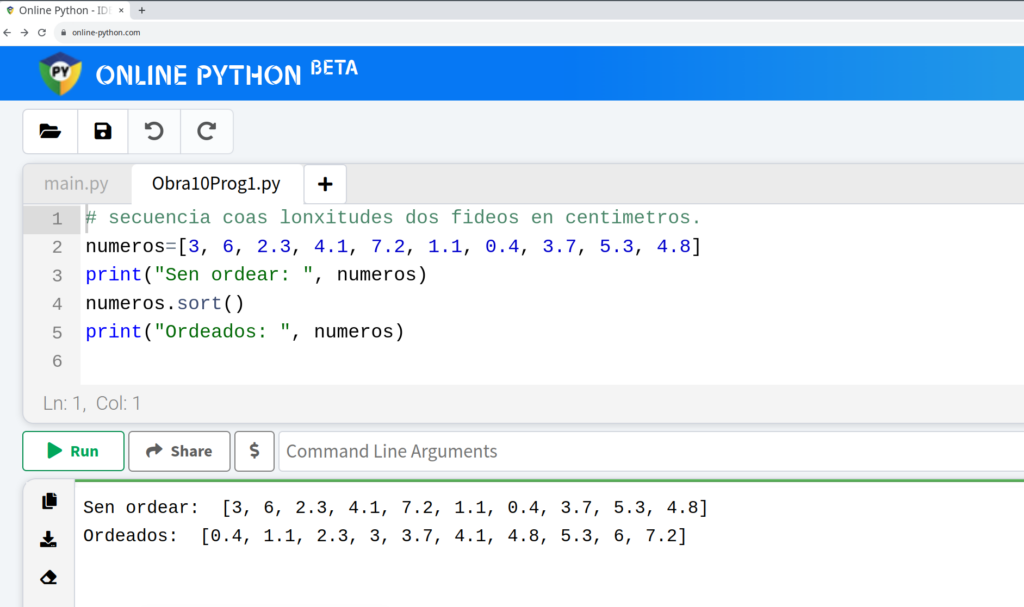
Figura 9. Exemplo para ordear unha colección de números usando a función sort(). Programa Obra10Prog1.py
Pero o alumnado terá interese en ver como funciona o ordenador cando a lista de números sexa realmente longa (por exemplo, 1000 valores). Cánsase o ordenador? Aínda que o exemplo da figura 9 é ilustrativo de como podemos realizar o ordenamento dunha colección de números en Python, é pouco práctico. Normalmente, queremos programas que fagan unha tarefa (ordear a colección de números) pero que ordee listas de números distintas cada vez que o executamos.
Podemos facer outro exercicio máis xenérico no que un programa xera automaticamente unha colección de “n” valores aleatorios no intervalo [1, 250] milímetros (que é a lonxitude máxima dun espagueti). Para simplificar, supoño que só xero números enteiros, ou sexa, que non podo cortar o espagueti con tamaños menores a un milímetro, e aplico o ordeamento a esta coleción ou lista. Podes visualizar o programa na figura 10 que se corresponde co programa Obra10Prog2.py. Este exercicio é adecuado para estudantes que estean aprendendo algúns conceptos de programación.
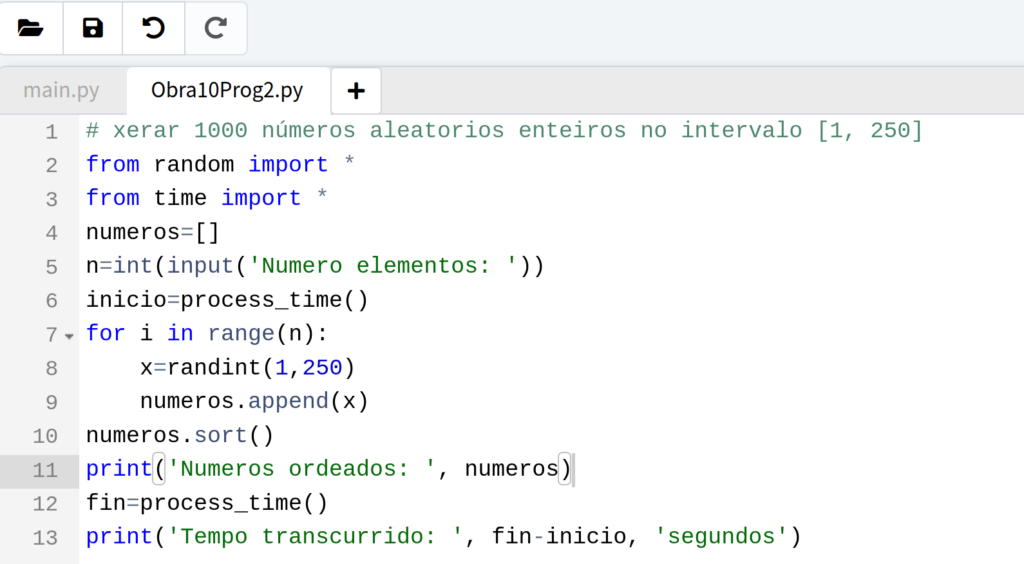
Figura 10. Idem que a figura 9 pero a colección de números xérase automáticamente e mídese o tempo necesario para realizar a tarefa. Programa no arquivo Obra10Prog2.py.
Na figura 10 o significado das liñas é o seguinte:
- A liña 1 é un comentario.
- A liña 2 carga na memoria do ordenador as funcións necesarias para xerar números aleatorios (fíxate que hai palabras resaltadas en azul indicando que estas palabras pertencen ó vocabulario de Python e teñen un significado). A función que utilizaremos do paquete random é randint().
- A liña 3 carga en memoria o paquete time con funcións para medir tempos de execución dos programas. Inclúe a función process_time() que devolve o tempo actual.
- A liña 4 introduce o personaxe de nome “numeros” e dálle o valor dunha colección baleira.
- A liña 5 pide por teclado o número de elementos da colección coa función input(). Cando se executa esta función o programa párase e agarda a que escribamos un número polo teclado do ordenador. Todo o que introducimos por teclado sempre se representa internamente como unha cadea de caracteres (un texto), e a función int() transforma o texto nun número enteiro, que lle dá valor ó personaxe con nome “n”. Repara en que todos os nomes de funcións de Python son palabras reservadas da linguaxe de programación (son o seu vocabulario) e aparecen resaltadas nunha cor distinta (neste caso en gris, aínda que a cor pode variar entre intérpretes de Python).
- A liña 6 introduce o personaxe “inicio” e dálle o valor do tempo actual coa función process_time().
- A liña 7 repite “n” veces, tantas como número de elementos na colección, coa repetición definida que vimos no obradoiro 9 (a palabra reservada for). A función range(n) xera unha colección de números que comezan en 0, rematan en n-1 e a distancia entre os números é 1, é dicir, [0, 1, 2, 3, …, n-1].
- As liñas 8 e 9 son o bloque de código (tarefas indivisibles e, polo tanto, pequeniñas) que se executa en cada repetición (chamada en informática “iteracción”). A liña 8 xera un número enteiro entre 1 e 250 coa función randint() e pono noutro personaxe chamado “x”. A liña 9 engade o valor de “x” á colección de elementos “numeros” coa función append().
- A liña 10 ordea a colección de elementos con nome “numeros”, igual que o programa anterior.
- A liña 11 amosa o contido de “numeros”. Se ten unha lonxitude moi grande, amosar este contido pode non ser boa idea e podemos comentar esta liña co símbolo # ó inicio da liña.
- A liña 12 introduce o personaxe “fin”, dándolle o valor do tempo actual. A liña 12 amosa o tempo transcurrido desde inicio a fin (fin-inicio) en segundos.
Imos ver como sería o algoritmo que utilizamos para ordear os fideos de espagueti sen utilizar a función sort(), é dicir, tal como fixemos antes manipulando os espaguetis. As profesionais da informática temos que saber escribir estas funcións. Podes medir os cachos de fideos coa regra se o alumnado é máis novo (porque lles adoita gustar manipular materiais) e poñer as medidas exactas en milímetros, pero tamén podemos aproximar a ollo as súas lonxitudes, como fixen no exemplo da figura 10 (reproducindo as lonxitudes dos fideos de espagueti da figura 1).
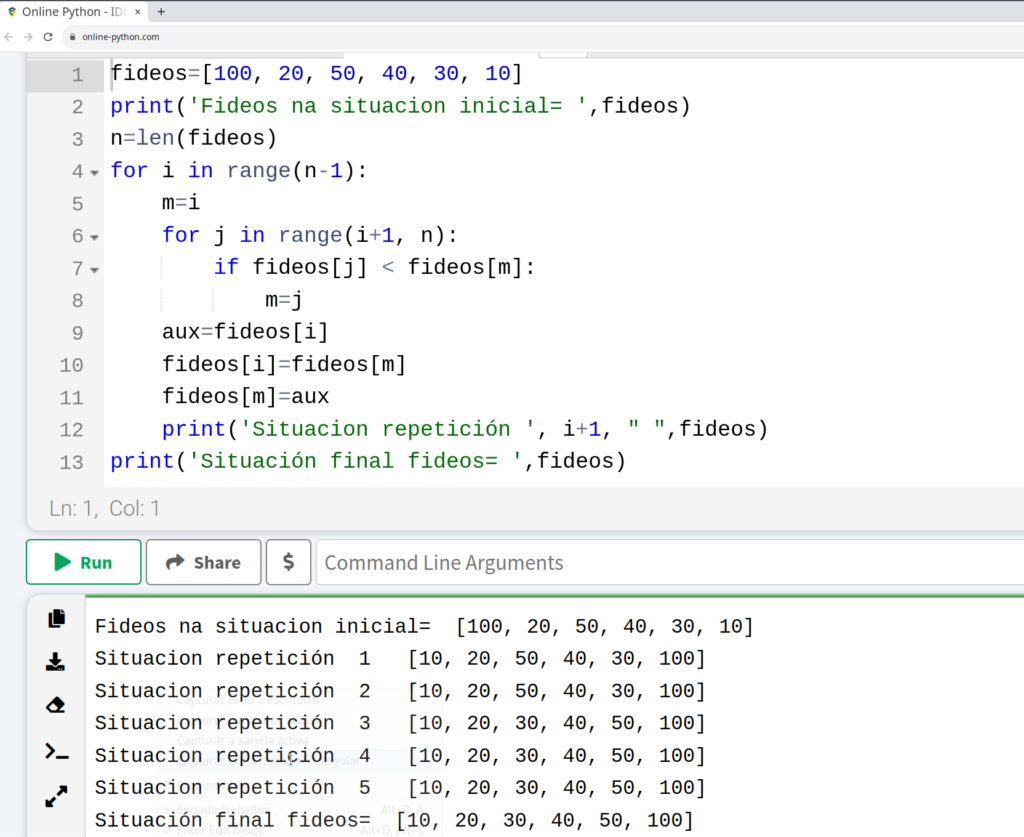
Figura 11. Programa en Python para ordear os fideos sen utilizar a función sort(). Programa no arquivo Obra10Prog3.py
A explicación do programa da figura 11 para o profesorado sería:
- A liña 1 introduce o personaxe “fideos” cos valores das lonxitudes dos fideos en milímetros (tecnicamente é unha colección ou lista de números e, polo tanto, ten que ir entre corchetes e cos número separados por comas, como nos din as regras da linguaxe Python).
- A liña 2 amosa na pantalla (cando executemos o programa) o contido da personaxe fideos coa función print().
- A liña 3 introduce o personaxe de nome “n” e dalle como valor a lonxitude da lista de números “fideos” utilizando a función de python len(), que calcula o número de elementos dunha lista ou colección.
- A liña 4: vimos cando manipulamos os fideos que repetiamos un proceso varias veces (tantas como fideos tiñamos sobre a mesa). Isto lémbranos ó mecanismo do obradoiro 8 de repeticións definidas (cando sabemos a priori cantas veces hai que repetir). Neste caso repetimos tantas veces como elementos ten a nosa colección menos un (porque sempre estamos comparando un fideo con outro), polo tanto, repetimos n-1 veces. De aí a frase: “for i in range(n-1):”. En realidade, o que pasa é que ao final o último elemento xa é sempre o máximo e non hai que ordealo. As liñas desde a 5 á 12 son as operacións (accións) que se fan en cada repetición ou iteracción. Neste caso o conxunto de tarefas é bastante complexo, non como en casos anteriores nos que só eran unha ou dúas liñas, pero iremos debullando polo miúdo que fai cada liña a continuación.
- A liña 5 introduce outro personaxe con nome “m” e dálle o valor “i”, pero… que é “i”? Pois “i” é outro personaxe que se introduce implicitamente na liña 4. A función range(n-1) xera a lista de números [0, 1, 2, 3, 4] (xa que n ten o valor 6), e o personaxe “i” toma o valor 0 na primeira repetición, 1 na segunda repetición, 2 na terceira repetición, e así sucesivamente. Polo tanto, vedes que este personaxe “m” fai o papel de sinalar o primeiro fideo comezando pola esquerda que non está ordeado (na primeira repetición do proceso é o primeiro elemento, pero Python sempre comeza a contar en 0 no canto de 1 como facemos as persoas).
- A liña 6: diciamos que unha vez que sinalamos un fideo, percorremos todos os fideos cara á dereita para atopar o que é máis curto. Aínda que é unha operación que as persoas facemos inconscientemente, se pensamos como facelo paso a paso dámonos conta de que comparamos a lonxitude do fideo en consideración (o fideo “m”) coa do seguinte fideo, despois co seguinte, e así sucesivamente. Este proceso implica unha repetición e polo tanto outra estrutura de repetición… cantas veces hai que repetir? Pois tantas como fideos queden para a dereita. Por iso a liña 6 contén a frase: “for j in range(i+1, n):” que introduce un novo personaxe, a “j” para ir collendo valores da lista que vai dende “i+1” (posición do fideo que está a dereita do fideo “i”) ata o final (o fideo final cara á dereita nas figura 2 a 7). As liñas 7 e 8 son as accións (tarefas indivisibles) que hai que repetir dentro desta estrutura de repetición.
- A liña 7 é unha estrutura de bifurcación como a que vimos no obradoiro 9, que permite comparar a lonxitude dos fideos nas posicións “m” (o fideo sinalado de máis á esquerda na figura 2) e “j” (frase “if fideos[j] < fideos[m]:”). A construción: nome personaxe de tipo colección, corchete, personaxes de posición, corchete. Por exemplo fideos[j] permite obter o valor da colección de lonxitudes “fideos” na posición “m” ou “j” (realmente comproba se a lonxitude do fideo na posición j é menor que a do fideo da posición “m”) e se esta condición se cumpre faise a liña 8, se non se cumpre saltaríase a liña 8. De aí que as bifurcacións fan que non teñan que executarse necesariamente todas as frases ou liñas do programa, igual que cando camiñamos pola cidade non podemos ir ó mesmo tempo por todas as rúas, dependerá do que queremos facer en cada momento, colleremos un camiño ou outro.
- A liña 8: esta frase serve para gardar no personaxe “m” a memoria (os recordos) xa que conserva a posición do fideo máis curto ata o momento no noso percorrido de esquerda a dereita para atopar o fideo máis curto. A partir de agora, compararemos os seguintes fideos con este, porque é o máis pequeno que atopamos ata agora.
- Liñas 9 a 11, ambas inclusive: a estas liñas chegamos cando deixamos de repetir as liñas 7 e 8, que é cando chegamos ó fideo de máis á dereita intentando atopar o fideo máis pequeno. Ese fideo máis curto entre o fideo sinalado (o de máis á esquerda que está na posición “i”) e o fideo de máis á dereita atópase na posición “m”. A tarefa que fixemos manipulando fideos foi intercambiar ambos fideos (o da posición “i” pasa á posición “m” e o da posición m pasa á posición i) pero… como fan este intercambio as máquinas? Imaxina que tes dúas pelotas: unha verde na man esquerda e unha azul na man dereita; queres intercambialas de man (poñer a verde na man dereita e a azul na man esquerda). Podes levar dúas bolas a clase para escenificar o problema. Como o facemos? Salvo que saiba facer malabarismos, necesito pedir axuda a alguén para que aguante unha da bolas mentres que mudo a outra bola de man, e despois xa lle pido que me dea a bola. Isto mesmo ten que facer o ordenador. A ese novo personaxe chameille “aux” no programa, que significa “auxiliar”.
- A liña 12 simplemente amosa o contido da colección de números en cada repetición.
- A liña 13 execútase despois de rematar todas as repeticións que comezaron na liña 4 e amosa o contido da colección de elementos de nome “numeros”.
Para que vos fagades unha idea da dificultade do problema que estivemos resolvendo, este algoritmo ensínase na universidade a finais do primeiro curso ou no segundo curso da titulación de Enxeñaría Informática, ou sexa a persoas de 18 ou 19 anos. Alumnado incluso 10 anos máis novo pode entendelo porque na informática non traballamos con conceptos moi difíciles. Moitas veces simplemente observamos as realidades cotiás da nosa vida.
Para o alumnado máis novo, poderías montar unha obra de teatro para escenificar ó algoritmo. Algunhas suxerencias: se na aula hai máis de 13-14 estudantes, dividila en dous grupos no que un grupo desenvolve a obra e o outro mira a obra e controla que non se equivoquen. Podes repetir o proceso intercambiando os grupos. Imaxina que estamos no recreo e todo o alumnado da aula colócase nunha fila para entrar na aula.
Por algún motivo (un evento, o que sexa), hoxe queremos que na fila o alumnado estea ordeado por estaturas, o máis baixo na cabeza de fila e o máis alto no final (cando eu fun nena colocábannos así). Pegunta ó alumnado como faría para, en pouco tempo, conseguir unha fila ordeada. Seguro que o fan moito máis rápido que utilizando o algoritmo que se describe aquí (como tamén o fan máis rápido cos fideos cando o número de fideos é baixo), porque a intelixencia humana é dun nivel moi superior ó de calquera máquina. Pero temos interese en facelo segundo as intrucións do algoritmo.
Imaxina que o personaxe “fideos”, que é unha colección de números coas lonxitudes dos fideos, agora chamámoslle fila e é como a máquina dun tren na que están enganchados varios vagóns (estudantes collidos da man), cada un cunha persoa con dous números (a súa estatura en centímetros e o número de vagón que é a súa posición en relación ó vagón máquina). O primeiro vagón é o estudante 0, porque en Python, como tamén os anos nos séculos, comezamos a contar en 0. De toda a equipa, quito algunhas persoas para interpretar outros papeis presentes no algoritmo da figura 10. Reparto de papeis:
- O personaxe “i” que lle cambio o nome a “sinaladora”.
- O personaxe “m” que lle cambio o nome a “MaisBaixa”.
- O personaxe “j” que lle cambio o nome a “buscadora”.
- O personaxe “aux” que agora chamo “cadeira”.
- Necesito un papel de narradora, que o pode facer o profesorado ou o personaxe “cadeira”.
Poñemos o tren no medio do escenario. “sinaladora” e “MaisBaixa” colócanse a carón do primeiro vagón do tren (persoa 0). “Buscadora” colócase no seguinte vagón (persoa 1), pregunta a “MaisBaixa” que estatura ten o seu estudante. Se a persoa do seu vagón ten menor estatura que a do vagón “MaisBaixa”, dille a “MaisBaixa” que se mude de vagón. Repite esta comprobación ate que chegue ó final do tren. Neste momento intervén quen fai o papel de narradora, “cadeira” ou outra persoa, para ordearlle a “sinaladora” que vaia a “cadeira”; a “MaisBaixa” que vaia a onde estaba “sinaladora”; e a “cadeira” que vaia a “MaisBaixa”.
Isto conclúe unha repetición para “sinaladora”. Na seguinte repetición, “sinaladora” ten que avanzar ó seguinte vagón. Aquí tamén volve “MaisBaixa” e no seguinte vagón “buscadora” e volvemos a repetir o proceso ate que “sinaladora” chegue ó penúltimo vagón do tren. Esta sería a esencia da obra de teatro, que poderiamos adornar con fantasía, incorporando diálogos cada vez que as personaxes “sinaladora”, “buscadora”, etc. chegan a un vagón novo.
