O problema formulado é calcular a distancia que percorre unha pelota cando a lanzamos co pé (ou coa man) co obxectivo de explicar como se deseñan os programas que utilizan aprendizaxe automática. A primeira parte do exercicio é adecuado para o alumnado de todos os niveis, e a segunda parte é para alumnado da ESO. Tamén pode ser interesante para o alumnado de bacharelato. Corresponde ó profesorado decidir ata onde chegar en función dos seus obxectivos e nivel educativo.
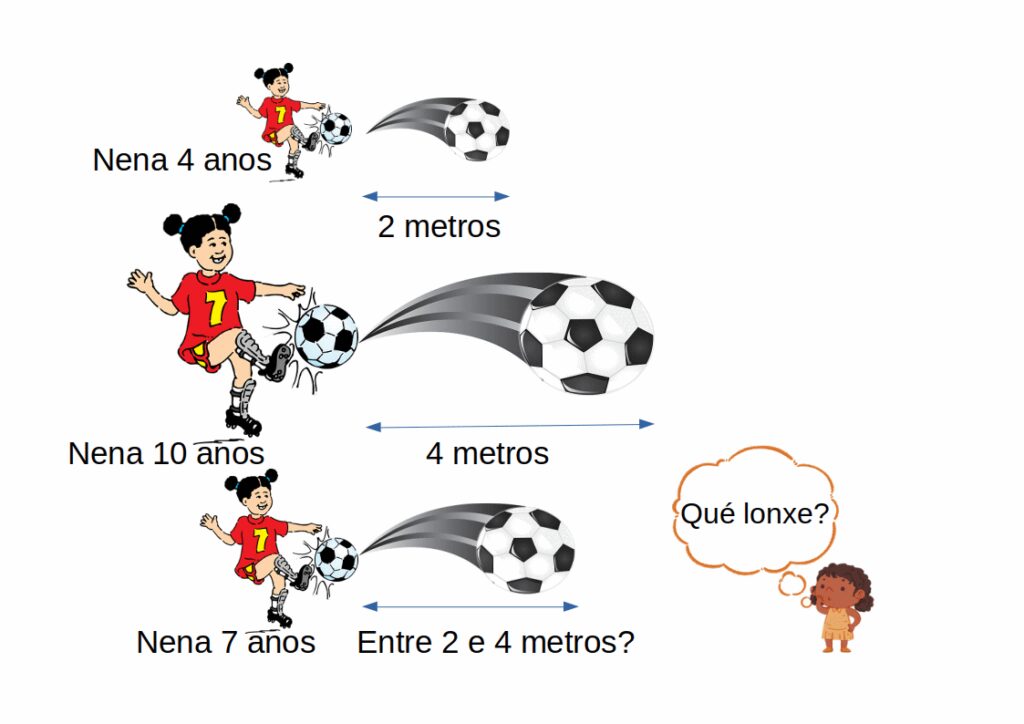
Figura 1: Nena lanzando unha pelota. Fonte: composición propia traducida do inglés da revista Frontiers of young minds
Na figura 1 observas a unha nena lanzando unha pelota. Como indica o gráfico, sabemos que unha nena de 5 anos lanzou a pelota a unha distancia de 2 metros, e unha nena de 10 anos lanzou a pelota a 4 metros. A pregunta é: a que distancia lanzará a pelota a nena de 7 anos? O alumnado non sabe a responta exacta aínda que, presumiblemente, sexa un valor entre 2 e 4 metros. Como podemos calcular esta distancia?
Imaxinando un escenario moi simplificado (pero que nos interesa desde o punto de vista educativo para entender a solución), vou supoñer que a distancia percorrida pola pelota é proporcional á idade da nena. Tamén para simplificar, vou chamar a idade co nome x e a distancia co nome y. Dicir que y é proporcional a x pode expresarse matematicamente como a ecuación dunha recta sen termo independente:
y=ax
Esta ecuación representa unha relación entre a distancia (y) e a idade (x). O termo de proporcionalidade é “a”, pero, polo momento, o valor de a é descoñecido e non podemos usar a ecuación para calcular a distancia. A ecuación define o algoritmo (esta ecuación denomínase habitualmente modelo na linguaxe da intelixencia artificial) que vou utilizar para resolver o problema pero, a diferencia do exercicio do ordeamento de fideos, non podo aplicalo porque ten un parámetro, o “a”, do que non coñezo o seu valor.
Como determinar o valor de a? O máis simple sería, dado que coñecemos o valor da distancia para dúas idades (tal como se amosa na táboa 1), considerar a recta que une eses dous puntos (tal como se observa na figura 2).

Táboa 1: Datos coñecidos de idade e distancia que percorre a pelota para dúas nenas
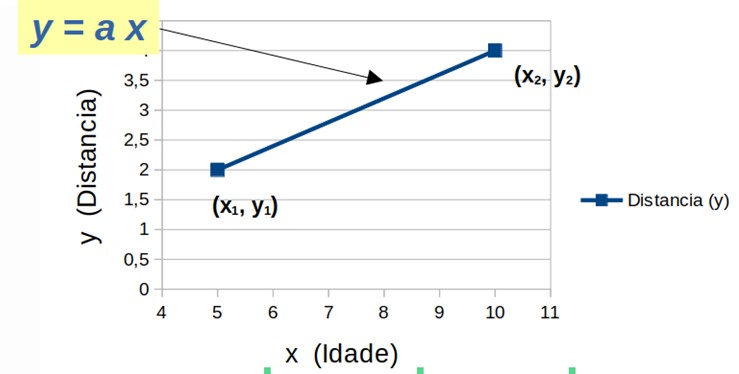
Figura 2. Recta que modela o noso problema
A ecuación desta recta pode calcularse coa fórmula (explicado na materia de matemáticas):
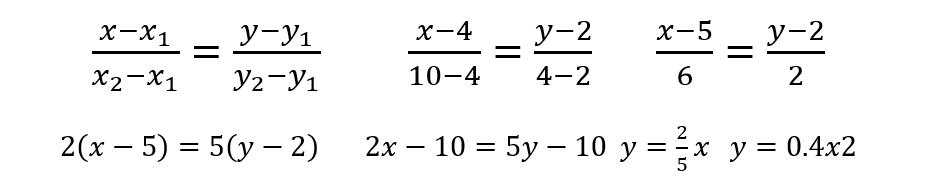
Polo tanto, o valor de a é 0.4 e a ecuación da recta y=0.4 x.
A este proceso na linguaxe da intelixencia artificial chámaselle adestramento, porque con el configuramos o modelo (ecuación da recta, definida polo valor a) utilizando exemplos coñecidos (neste caso a distancia que percorre a pelota para dúas nenas de distintas idades). Ó resultado chámaselle modelo entrenado, e permite estimar ou predicir a distancia que vai percorrer a pelota para unha nena con unha idade distinta, simplemente aplicando a ecuación da recta. Fíxate en que estamos supoñendo que a relación entre idade (x) e distancia (y) é y=ax.
Funcionan sempre ben os modelos entrenados? Nada garante que funcione ben. As causas poden ser varias:
- Que as propiedades usadas como entrada non teñan información suficiente para modelar o problema. Tal vez a distancia que percorre a pelota dependa doutros factores como o peso da pelota, o peso da persoa ou incluso o sexo.
- Que as medidas que fixen do problema (medidas das nenas de 5 e 10 anos) non sexan representativas do problema. Entón, considerando máis exemplos (máis persoas e máis variadas) podo mellorar a configuración do modelo.
- Que o meu modelo sexa moi simple para modelar o problema. No canto dunha recta tería que utilizar outro tipo de función de curva ou outro modelo distinto.
Polo tanto, despois de deseñar o modelo (calculando todos os parámetros que o configuran… nesta caso o valor de a), terei que probalo para comprobar se realiza o seu traballo con calidade. Na aula podes facer a seguinte proba: pide ó alumnado que calcule a distancia á que lanzarían a pelota os membros da súa familia. Nun caso ficticio, miña mai con 35 anos lanzaría a pelota a 35 x 0.4=14 metros, meu irmán con 15 anos lanzaría a pelota a 15 x 0.4=6 metros, meu avó con 70 anos lanzaría a pelota a 70 x 0.4=28 metros, miña bisavoa con 92 anos lanzaría a pelota con 92 x 0.4=36 metros. Cres que istos valores reflicten a realidade?
Debate co alumnado pero claramente non. Entre outras cousas porque o modelo non foi entrenado con persoas adultas e podemos ver como o seu funcionamento, sobre todo coa xente de maior idade, é disparatado. Se fose unha persoa ó ver ese resultado disparatado non o diría e calaría, pero a intelixencia artificial sempre responde, aínda que sexa algo sen sentido.
Imos a complicar un pouco o noso modelo. O alumnado de educación primaria podería parar aquí, porque non coñece os conceptos matemáticos que seguen…. pero o alumnado da ESO xa o pode facer. En vez de recompilar o lanzamento da pelota para dúas persoas, podemos recompilar máis exemplos, tal como se amosa na figura 3. É simplemente un exemplo ilustrativo con datos de idade e distancia para cada persoa inventados. Como calcular a mellor recta que modela esos datos? A recta elixida é aquela que minimiza a distancia dos puntos á recta, considerando que as distancias dos puntos dun lado da recta suman e as do outro lado restan. Para propósitos avanzados, deixo o programa de Python que xa ten funcións para calcular a ecuación da recta. Poderás descargar o arquivo aquí.
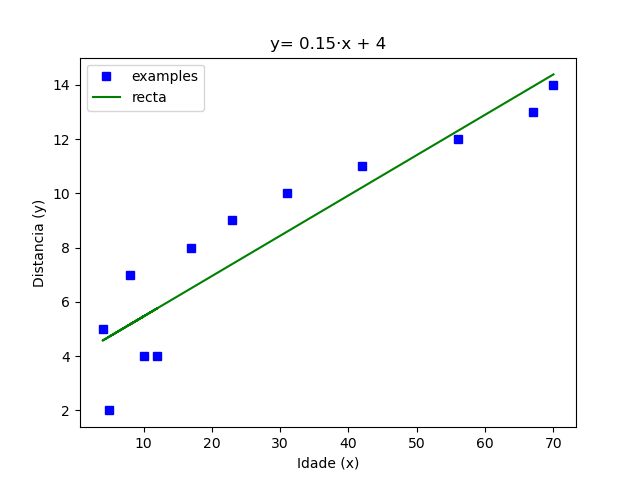
Figura 3. Ecuación da recta cando consideramos varios exemplos de persoas con (idade,distancia)
Podemos observar que este modelo podería non funcionar porque a idade pode non ser información suficiente para modelar o problema, é dicir, para calcular a distancia.
Imaxina que engadimos como dato de entrada a maiores o peso da pelota. Entón a distancia que percorre a pelota (y) dependería de dúas propiedades: a idade (que chamo x1) e o peso (que chamo x2). A formula do modelo supoñendo que a distancia é proporcional as dúas entradas sería:
y=ax1+bx2
no que “a” e “b” son os datos a determinar no proceso de adestramento para poder utilizar o modelo. Necesito, como mínimo, dúas persoas cos seus datos de idade, peso e distancia. Parto dos datos inventados da táboa 2.
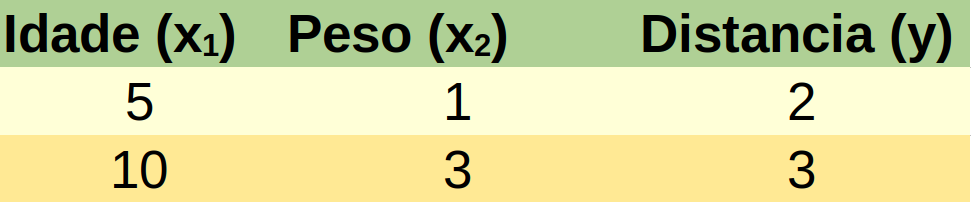
Táboa 2: Exemplos de idade, peso e distancia da pelota para o entrenamento do modelo
Teremos que resolver o sistema de ecuacións lineais:
2 = 5a + b
3 = 10a + 3b
O alumnado pode resolver este sistema de ecuacións e obter o resultado: b=-1 e a=0.6.
Con estos valores xa temos o modelo adestrado e podemos utilizalo para predicir a distancia á que lanza a pelota outra persoa. Igual que no caso anterior, podemos preguntarnos se fai ben o traballo para o que foi adestrado o modelo. Probablemente a resposta siga sendo non. É probable que se necesite incorporar máis propiedades ou que se necesiten modelos máis sofisticados para aprender este problema. Ou utilizar máis datos de exemplo, é dicir, máis nenas e nenos cos seus datos de idade e peso da pelota e as súas distancias.
Como poderíamos saber se funciona ou nou o noso modelo adestrado? Pois comparando a distancia calculada polo modelo para outras persoas (non usadas para adestrar o modelo) coas distancias verdadeiras para esas persoas, e vendo se son iguais ou non. Canto máis grande sexa a diferencia entre as distancias calculadas e verdadeiras, peor funciona o modelo; se a diferenza é pequena o modelo funciona ben.
Xa podemos dicir que coñecemos os mecanismos básicos que utilizan as persoas que deseñan os sistemas de intelixencia artificial.
En resumo, necesítase utilizar a intelixencia artificial ou programas con aprendizaxe automática cando non somos capaces de inventar un algoritmo que, a partir das entradas, calcule a saída do programa. En certo modo, a intelixencia artificial é unha chapuza para resolver, de xeito aproximado, un problema. Sempre que sexa posible obter solucións exactas ó problema, como no caso do ordeamento dos fideos de espaguetis, a solución é moito máis elegante e precisa, xa que funciona (acerta) sempre. Así, a intelixencia artificial, que xa vemos que non é intelixente, é unha forma de recoñecer o noso fracaso na definición de algoritmos e estratexias complexas.
